材料力学基础知识

在实际应用中，经常会遇到零件的刚性要求，通俗来说就是指在某些条件下，材料不能被破坏，或者最大变形不能超过某个值。那从技术指标上看，是用哪些量来衡量？如何利用这些量来判定的呢？

• 强度要求：在规定载荷作用下的构件不应破坏；
• 刚度要求：构件应有足够抵抗变形的能力；
• 稳定性要求：构件应有足够保持原有平衡形态的能力。

其中，变形的基本形式包括拉伸、压缩、剪切、扭转和弯曲等。

上图为一般拉伸应力-应变曲线，通常可以通过拉伸测试得到。那么从应力-应变曲线中，可以获取哪些信息呢？

首先，材料拉伸可以分为4个阶段：即弹性阶段–屈服阶段–强化阶段–局部变形阶段。图中ob 为弹性阶段，此阶段遵循胡克定律，即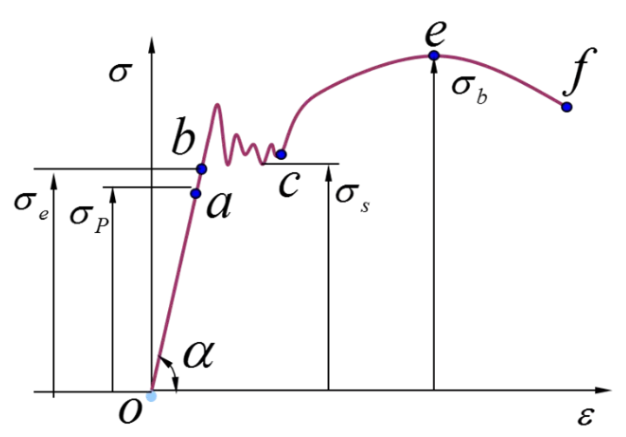

其中，E 为拉伸弹性模量（或杨氏模量），b 点的应力为弹性极限；bc 段为屈服阶段，此阶段失去了抵抗变形的能力，c 点的应力为屈服极限；ce 段为强化阶段，此阶段恢复了抵抗变形的能力，最高点e 点的应力为强度极限；ef 段为局部变形阶段，此阶段横向尺寸会突然急剧减小，直至断裂。

当然，不是所有的材料都有明显的4个阶段，例如有些脆性材料的屈服阶段、强化阶段会很小。所以，对于未知材料需要通过测试来获取这些参数，从而加深对材料的认识。

通过以上内容，我们得知脆性材料断裂时的应力为强度极限σb，塑性材料屈服的应力为屈服极限σs，这两个参数为构件失效时的极限应力。在工程中会根据材料的不同，考虑不同的安全因数。极限应力与安全因数的比值为许用应力[σ]。为了保证构件能正常工作，其工作应力σ 必须小于许用应力[σ]。

以下为某项目顶蓬局部应力计算结果，已知此材料的屈服强度为7.5MPa，判断所显示区域是否有失效风险。

当安全因数为1.5时，此材料的许用应力为5MPa。从图中可知，橙色和红色部分的应力大于5MPa。可以判定，这些区域有失效风险。

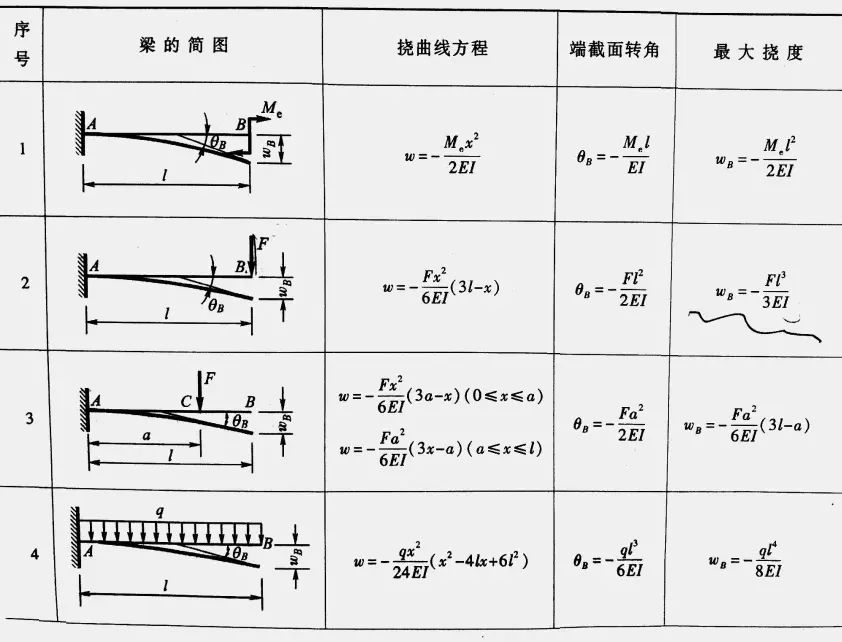
在材料力学中，通俗上所说的弯曲变形又称挠度，定义为在受力或非均匀温度变化时，杆件轴线在垂直于轴线方向的线位移，或板壳中面在垂直于中面方向的线位移，其英文为Deflection。运用叠加法可以推导出梁在简单载荷作用（包括悬臂、简支等）下的变形，下图列出了部分公式^[1]：

表1 梁在简单载荷作用下的变形

以上表中的2号结构为例，对于长度为l 的悬臂梁，在自由端施加力F，其最大挠度为：

其中，EI 为梁的抗弯刚度，E 为材料的弹性模量，I 为截面惯性矩，与截面形状有关。

从上式可以得出：若要减小最大挠度，可以减小力F，或减小梁的长度l，或增加材料的弹性模量E，或增加截面惯性矩I。